在数学的广袤天地中，二重积分极坐标转换公式就像是一把神奇的钥匙，能够为我们打开许多复杂问题的解题之门，对于很多学习数学的朋友来说，这个公式可能既神秘又令人充满好奇，就让我们一起深入这个奇妙的世界，去揭开它神秘的面纱。

想象一下，我们在一个平面上有一块区域，需要计算它的面积或者与面积相关的某些量，传统的直角坐标系可能会让计算变得繁琐复杂，而这时候，二重积分极坐标转换公式就闪亮登场了。

二重积分极坐标转换公式是什么呢？它的表达式为：\(\int\int_{D}f(x,y)dxdy = \int_{\alpha}^{\beta}\int_{r_1(\theta)}^{r_2(\theta)}f(rcos\theta,rsin\theta)rdrd\theta\) 。

这里的 \(r\) 表示极径，\(\theta\) 表示极角，\(\alpha\) 和 \(\beta\) 分别是极角的下限和上限，\(r_1(\theta)\) 和 \(r_2(\theta)\) 则是极径的下限和上限。

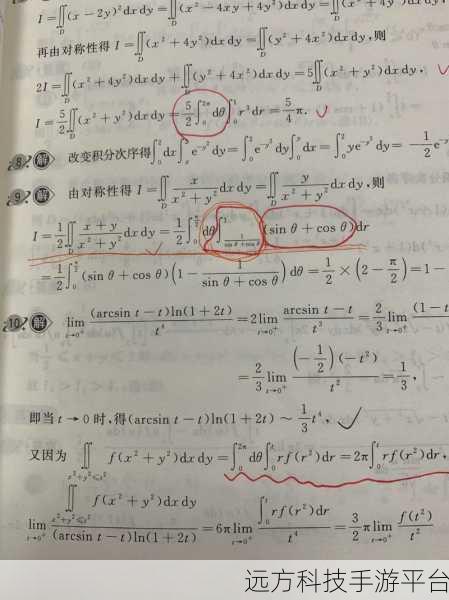
为了更好地理解这个公式，我们来看一个具体的例子，假设我们要计算一个以原点为圆心，半径为 \(R\) 的圆形区域上的某个函数的二重积分，在直角坐标系下，这个计算可能会相当复杂，但如果我们转换到极坐标系，那么这个区域就可以简单地表示为 \(0\leq\theta\leq 2\pi\)，\(0\leq r\leq R\) 。

再比如，当函数 \(f(x,y)\) 具有某些特殊的对称性时，使用极坐标转换公式往往能大大简化计算，如果函数关于 \(x\) 轴或 \(y\) 轴对称，或者关于原点对称，那么在极坐标系下可能会更容易发现规律。

让我们通过一个小游戏来加深对二重积分极坐标转换公式的理解。

游戏名称：“极坐标大冒险”

游戏玩法：

1、准备一些具有不同形状和函数的题目卡片，比如圆形、扇形、环形区域上的简单函数。

2、将参与者分成小组，每个小组轮流抽取题目卡片。

3、小组需要在规定时间内，使用二重积分极坐标转换公式计算出给定区域上函数的积分值。

4、计算完成后，其他小组可以进行检查和讨论，确保答案的正确性。

5、得分最高的小组获胜。

通过这个游戏，不仅可以增加对二重积分极坐标转换公式的熟练运用，还能在团队合作中体会到数学的乐趣。

下面是几个与二重积分极坐标转换公式相关的问答：

问：在什么情况下使用二重积分极坐标转换公式更方便？

答：当积分区域具有圆形、扇形或者环形等特点，以及函数具有某种对称性时，使用极坐标转换公式通常会使计算更加简便。

问：如何确定极坐标中的积分上下限？

答：根据积分区域的边界在极坐标下的表达式来确定，对于一个以原点为圆心，半径为 \(R\) 的圆，极径 \(r\) 的范围就是 \(0\) 到 \(R\)，极角 \(\theta\) 的范围通常是 \(0\) 到 \(2\pi\) 。

问：二重积分极坐标转换公式与直角坐标转换公式有什么联系？

答：它们都是用于计算平面区域上的积分，只是在不同的坐标系下采用了不同的表达方式，直角坐标系更直观地描述矩形区域，而极坐标系更适合处理圆形或扇形区域，在某些情况下，可以通过坐标变换在两者之间灵活切换，以达到简化计算的目的。